* Calculator (check batteries)
* Tracing paper
* Straight edge (or ruler)
* Protractor
* Three 3x5 cards (both sides)
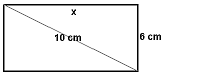 b)
b) 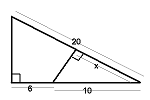 c)
c) 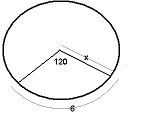 2. Consider the three dimensional figure below.
2. Consider the three dimensional figure below.
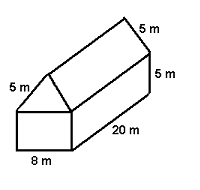 a) Find the volume ( 6 points )
b) Find the total surface area. ( 8 points )
3. Evaluate the following: ( 4 points each )
a. 9! - 5!
b. 22!
19! 3!
4. Consider this figure.
a) Find the volume ( 6 points )
b) Find the total surface area. ( 8 points )
3. Evaluate the following: ( 4 points each )
a. 9! - 5!
b. 22!
19! 3!
4. Consider this figure.
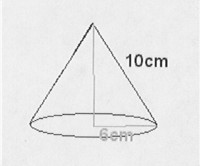 a) This is a ______________. ( 2 points )
b) Find the height. ( 5 points )
c) Find the volume. ( 5 points )
5. Tell the number of faces, edges, and verticies for the pictured 3-D shape. ( 4 points )
a) This is a ______________. ( 2 points )
b) Find the height. ( 5 points )
c) Find the volume. ( 5 points )
5. Tell the number of faces, edges, and verticies for the pictured 3-D shape. ( 4 points )
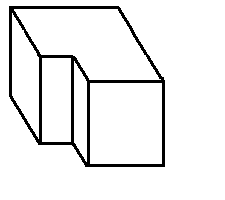 F
V
E
This is a __________________
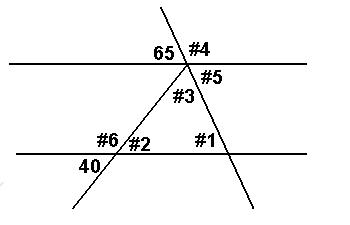
6. Measure each of the following angles. ( 3 points each )
F
V
E
This is a __________________
6. Measure each of the following angles. ( 3 points each )
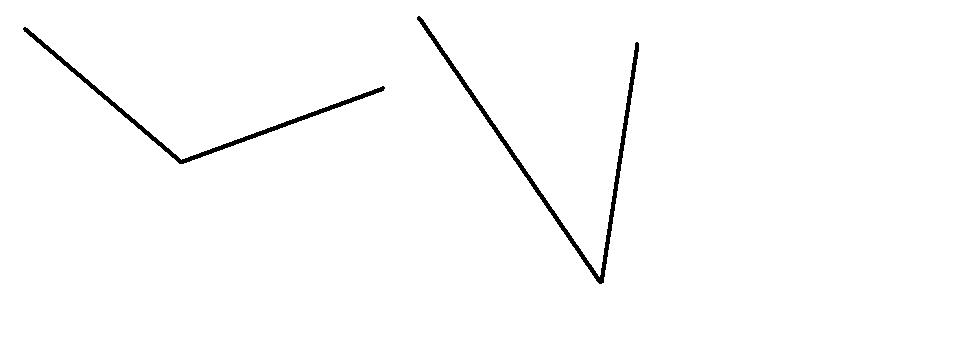
 Shift right 2 & up 3.
b)
Shift right 2 & up 3.
b) 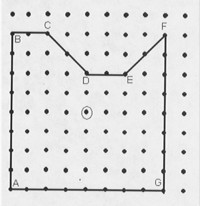 Shrink about the point O by 3/4.
c)
Shrink about the point O by 3/4.
c) 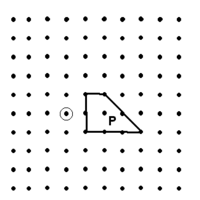 Rotation clockwise of 90° about the point O.
d)
Rotation clockwise of 90° about the point O.
d) 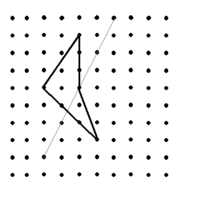 Reflection in the indicated line.
16. Consider a tournament with the best 2 out of 3 winning where the probability
that Chicago wins a given game is 2/3.
a) Draw the probability tree diagram for this tournament, and
label the probabilities for each branch. ( 6 points )
b) Determine the probability of Chicago winning at least
two games. ( 3 points )
c) Determine the probability that the tournament ends after
two games. ( 3 points )
17. Below there are three problems. Each has three sets of data and a description which fits one or
more of those sets of data. Choose the set(s) that fit each description ( 5 points each )
Reflection in the indicated line.
16. Consider a tournament with the best 2 out of 3 winning where the probability
that Chicago wins a given game is 2/3.
a) Draw the probability tree diagram for this tournament, and
label the probabilities for each branch. ( 6 points )
b) Determine the probability of Chicago winning at least
two games. ( 3 points )
c) Determine the probability that the tournament ends after
two games. ( 3 points )
17. Below there are three problems. Each has three sets of data and a description which fits one or
more of those sets of data. Choose the set(s) that fit each description ( 5 points each )
I. The data has a mean of 8 and a median of 5.
i 16, 4, 5, 14, 8, 4, 5 ii 3, 4, 9, 8, 1 iii 2, 3, 8, 2, 5II. The data has a mode of 8 and a median of 5.
i 1 , 8 , 6 , 3 , 8 , 3 , 9 , 2 , 5 , 8 , 6 ii 2 , 3 , 8 , 5 , 8 , 4 , 1 , 3 , 9 , 6 , 8 iii 3 , 6 , 9 , 4 , 3 , 8 , 8 , 5 , 3III. The data has a mean of 8 and a mode of 5.
i 2 , 9 , 17 , 5 , 12 , 4 , 8 , 19 , 6 , 5 , 13 ii 3 , 8 , 19 , 4 , 5 , 20 , 2 , 4 , 7 iii 8 , 18 , 4 , 5 , 15 , 9 , 5 , 3 , 5 18. For a regular six sided die the results of a number of rolls are in the rable below. ( 4 points each ) a) According to the table, how many times were the dice rolled?
b) According to the table, what is the probability of rolling a 2
on the die in this experiment?
c) What is the probability of rolling a 2
on a fair die (or the theoretical probability)?
d) Do you think that the die is a fair die? Explain ______
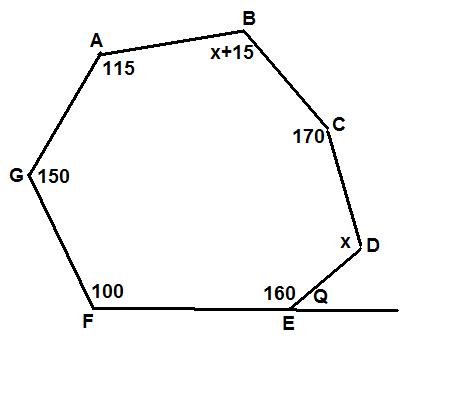
19. Find the perimiter and area of the below figure.
( 6 points each )
a) According to the table, how many times were the dice rolled?
b) According to the table, what is the probability of rolling a 2
on the die in this experiment?
c) What is the probability of rolling a 2
on a fair die (or the theoretical probability)?
d) Do you think that the die is a fair die? Explain ______
19. Find the perimiter and area of the below figure.
( 6 points each )
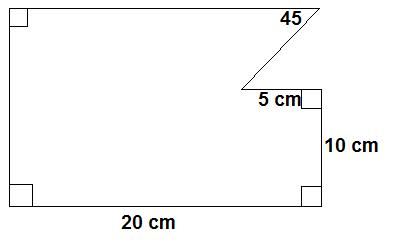 a) Perimiter _________
b) Area __________
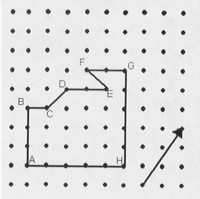
20. Sketch the following six shapes on the isodot paper. ( 5 points each )
a) A kite that is not a parallelogram.
a) Perimiter _________
b) Area __________
20. Sketch the following six shapes on the isodot paper. ( 5 points each )
a) A kite that is not a parallelogram.
 b) An isosceles trapezoid.
b) An isosceles trapezoid.
 c) A rhombus that is not a rectangle.
c) A rhombus that is not a rectangle.
 d) An obtuse scalene triangle.
d) An obtuse scalene triangle.
 e) A non-convex hexagon.
e) A non-convex hexagon.
 f) A parallelogram that is not a rectangle.
f) A parallelogram that is not a rectangle.

This page updated by Frank Matthews April 30, 2009